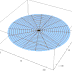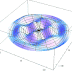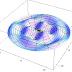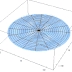
Bessel Function of Type 1

 

Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation 

for an arbitrary complex number α \alpha , which represents the order of the Bessel function. Although α \alpha and − α -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of α \alpha .

The most important cases are when α \alpha is an integer or half-integer. Bessel functions for integer α \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer α \alpha are obtained when solving the Helmholtz equation in spherical coordinates. 

The Bessel function is a generalization of the sine function. It can be interpreted as the vibration of a string with variable thickness, variable tension (or both conditions simultaneously); vibrations in a medium with variable properties; vibrations of the disc membrane, etc.

Bessel's equation arises when finding separable solutions to Laplace's equation and the Helmholtz equation in cylindrical or spherical coordinates. Bessel functions are therefore especially important for many problems of wave propagation and static potentials. In solving problems in cylindrical coordinate systems, one obtains Bessel functions of integer order (α = n); in spherical problems, one obtains half-integer orders (α = n + 1/2). For example:

•     Electromagnetic waves in a cylindrical waveguide
•     Pressure amplitudes of inviscid rotational flows
•     Heat conduction in a cylindrical object
•     Modes of vibration of a thin circular or annular acoustic membrane (such as a drumhead or other membranophone) or thicker plates such as sheet metal (see Kirchhoff–Love plate theory, Mindlin–Reissner plate theory)
•     Diffusion problems on a lattice
•     Solutions to the radial Schrödinger equation (in spherical and cylindrical coordinates) for a free particle
•     Solving for patterns of acoustical radiation
•     Frequency-dependent friction in circular pipelines
•     Dynamics of floating bodies
•     Angular resolution
•     Diffraction from helical objects, including DNA
•     Probability density function of product of two normally distributed random variables[1]
•     Analyzing of the surface waves generated by microtremors, in geophysics and seismology.

Bessel functions also appear in other problems, such as signal processing (e.g., see FM audio synthesis, Kaiser window, or Bessel filter).